Une matrice de confusion constitue un outil essentiel pour évaluer l’efficacité des algorithmes de classification dans le domaine de l’apprentissage automatique supervisé.
Qu’est-ce qu’une matrice de confusion ?
La perception humaine est subjective : même la distinction entre la vérité et le mensonge varie d’une personne à l’autre. Une ligne de 10 cm peut apparaître comme une ligne de 9 cm pour quelqu’un d’autre. La mesure réelle pourrait être 9, 10 ou une autre valeur. Notre estimation est la valeur prédite !
Tout comme notre cerveau utilise sa propre logique pour effectuer des prédictions, les machines appliquent divers algorithmes d’apprentissage automatique pour obtenir une valeur prédite. Ces valeurs peuvent être identiques ou différentes de la valeur réelle.
Dans un environnement compétitif, il est crucial de déterminer si nos prédictions sont correctes pour évaluer nos performances. De la même manière, nous pouvons évaluer l’efficacité d’un algorithme d’apprentissage automatique en fonction du nombre de prédictions justes qu’il a réalisées.
Alors, qu’est-ce qu’un algorithme d’apprentissage automatique ?
Les machines s’efforcent de résoudre des problèmes en appliquant une logique ou un ensemble d’instructions, connues sous le nom d’algorithmes d’apprentissage automatique. On distingue trois principaux types d’algorithmes d’apprentissage automatique : supervisés, non supervisés et par renforcement.
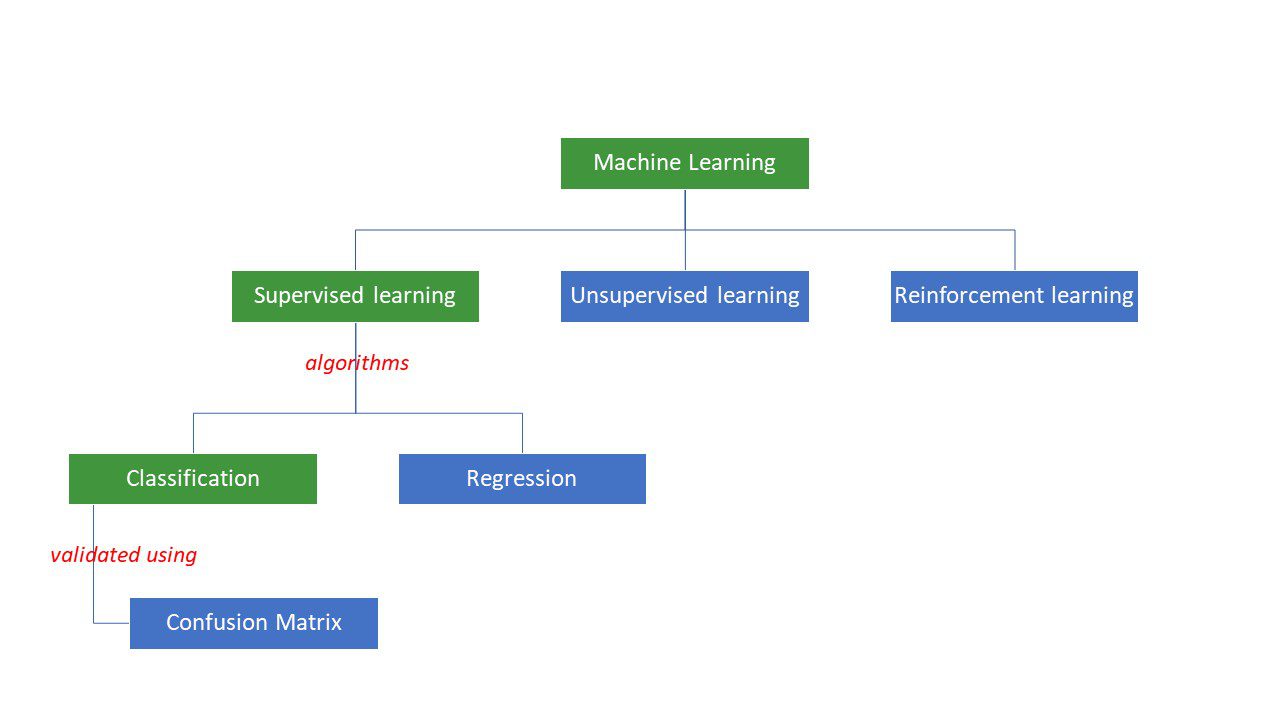
Les algorithmes supervisés sont les plus simples. Dans ce type d’apprentissage, nous connaissons déjà la réponse. Les machines sont entraînées pour atteindre cette réponse en utilisant un grand nombre de données. C’est un peu comme un enfant qui apprend à différencier des personnes de différents groupes d’âge en observant leurs caractéristiques de manière répétée.
Les algorithmes d’apprentissage automatique supervisé se divisent en deux catégories : la classification et la régression.
Les algorithmes de classification sont conçus pour classer ou trier des données selon des critères prédéfinis. Par exemple, si vous souhaitez que votre algorithme regroupe les clients en fonction de leurs préférences alimentaires (ceux qui aiment la pizza et ceux qui ne l’aiment pas), vous utiliserez un algorithme de classification tel qu’un arbre de décision, une forêt aléatoire, un classificateur bayésien naïf ou une machine à vecteurs de support (SVM).
Lequel de ces algorithmes est le plus performant ? Pourquoi choisir un algorithme plutôt qu’un autre ?
C’est là que la matrice de confusion intervient…
Une matrice de confusion est un tableau qui fournit des informations sur la précision d’un algorithme de classification lors du tri d’un ensemble de données. Son nom n’est pas destiné à nous induire en erreur ; cependant, un nombre élevé de prédictions incorrectes indique généralement que l’algorithme est confus !
En résumé, la matrice de confusion est une méthode d’évaluation des performances d’un algorithme de classification.
Comment cela fonctionne-t-il ?
Imaginez que vous ayez appliqué différents algorithmes à notre problème binaire mentionné précédemment : classer les individus selon qu’ils aiment ou non la pizza. Pour déterminer quel algorithme produit les valeurs les plus proches de la vérité, vous utiliserez une matrice de confusion. Pour un problème de classification binaire (j’aime/je n’aime pas, vrai/faux, 1/0), la matrice de confusion génère quatre valeurs distinctes :
- Vrai positif (VP)
- Vrai négatif (VN)
- Faux positif (FP)
- Faux négatif (FN)
Quelles sont les quatre composantes d’une matrice de confusion ?
Les quatre valeurs issues de la matrice de confusion constituent les composantes de cette dernière.
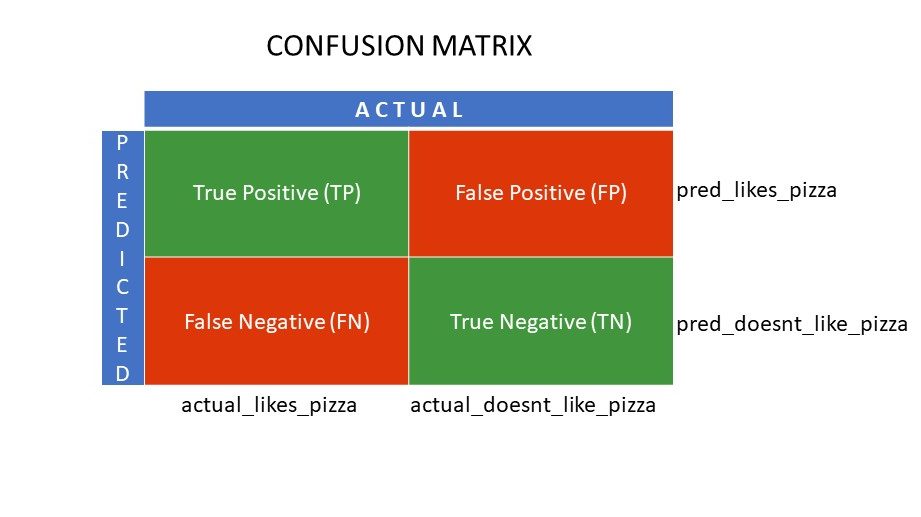
Les valeurs Vrai Positif (VP) et Vrai Négatif (VN) représentent les prédictions correctes de l’algorithme de classification :
- VP correspond à ceux qui aiment la pizza et que le modèle a correctement identifiés.
- VN correspond à ceux qui n’aiment pas la pizza et que le modèle a correctement identifiés.
Les valeurs Faux Positif (FP) et Faux Négatif (FN) représentent les prédictions erronées du classificateur :
- FP correspond à ceux qui n’aiment pas la pizza (négatif), mais que le classificateur a classés à tort comme aimant la pizza (positif). FP est également appelé erreur de type I.
- FN correspond à ceux qui aiment la pizza (positif), mais que le classificateur a classés à tort comme n’aimant pas la pizza (négatif). FN est également appelé erreur de type II.
Pour mieux comprendre ce concept, examinons un scénario réel.
Imaginons un ensemble de données de 400 personnes ayant subi un test Covid. Vous disposez des résultats obtenus grâce à divers algorithmes qui ont déterminé le nombre de personnes positives et négatives au Covid.
Voici deux matrices de confusion à titre de comparaison :
En les examinant, on pourrait être tenté de conclure que le premier algorithme est plus précis. Cependant, pour obtenir un résultat concret, il nous faut des indicateurs permettant d’évaluer la justesse, la précision et d’autres valeurs démontrant la supériorité d’un algorithme par rapport à un autre.
Indicateurs basés sur la matrice de confusion et leur importance
Les principaux indicateurs qui nous aident à déterminer si le classificateur a réalisé les bonnes prédictions sont les suivants :
#1. Rappel/Sensibilité
Le rappel, la sensibilité, le taux de vrais positifs (TVP) ou la probabilité de détection est le rapport entre les prédictions positives correctes (VP) et le total des positifs (c’est-à-dire VP et FN).
R = VP/(VP + FN)
Le rappel évalue le nombre de résultats positifs corrects obtenus par rapport au nombre total de résultats positifs qui auraient pu être produits. Une valeur de rappel élevée signifie que le nombre de faux négatifs est faible, ce qui est avantageux pour l’algorithme. Le rappel est utilisé lorsque la connaissance des faux négatifs est importante. Par exemple, si une personne a de multiples blocages cardiaques et que le modèle indique qu’elle est en parfaite santé, cela pourrait être fatal.
#2. Précision
La précision mesure les résultats positifs corrects parmi tous les résultats positifs prédits, y compris les vrais et les faux positifs.
Pr = VP/(VP + FP)
La précision est essentielle lorsque les faux positifs ont des conséquences majeures. Par exemple, si une personne n’est pas diabétique, mais que le modèle l’indique et que le médecin prescrit des médicaments, cela peut entraîner des effets secondaires graves.
#3. Spécificité
La spécificité ou taux de vrais négatifs (TVN) correspond aux résultats négatifs corrects obtenus parmi tous les résultats qui auraient pu être négatifs.
S = VN/(VN + FP)
Elle mesure la capacité de votre classificateur à identifier les valeurs négatives.
#4. Justesse
La justesse est le nombre de prédictions correctes rapporté au nombre total de prédictions. Si vous avez correctement trouvé 20 valeurs positives et 10 valeurs négatives à partir d’un échantillon de 50, la justesse de votre modèle sera de 30/50.
Justesse A = (VP + VN)/(VP + VN + FP + FN)
#5. Prévalence
La prévalence mesure le nombre de résultats positifs obtenus par rapport à l’ensemble des résultats.
P = (VP + FN)/(VP + VN + FP + FN)
#6. Score F
Il est parfois difficile de comparer deux classificateurs (modèles) en utilisant uniquement la précision et le rappel, qui sont des moyennes arithmétiques d’une combinaison des quatre composantes. Dans de tels cas, on peut utiliser le score F ou le score F1, qui est la moyenne harmonique, ce qui est plus précis, car sa valeur ne varie pas trop en cas de valeurs extrêmes. Un score F plus élevé (max 1) indique un meilleur modèle.
Score F = 2*Précision*Rappel / (Rappel + Précision)
Lorsque la gestion des faux positifs et des faux négatifs est primordiale, le score F1 est un bon indicateur. Par exemple, ceux qui ne sont pas positifs au Covid (mais que l’algorithme a indiqué comme tels) n’ont pas besoin d’être isolés inutilement. De même, ceux qui sont positifs au Covid (mais que l’algorithme a indiqués comme négatifs) doivent être isolés.
#7. Courbes ROC
Des paramètres tels que la justesse et la précision sont de bons indicateurs si les données sont équilibrées. Pour un ensemble de données déséquilibré, une justesse élevée n’implique pas nécessairement que le classificateur est efficace. Par exemple, si 90 étudiants sur 100 dans un groupe connaissent l’espagnol, même si votre algorithme indique que les 100 le connaissent, sa justesse sera de 90 %, ce qui peut donner une image faussée du modèle. En cas d’ensembles de données déséquilibrés, des indicateurs comme le ROC sont plus efficaces.
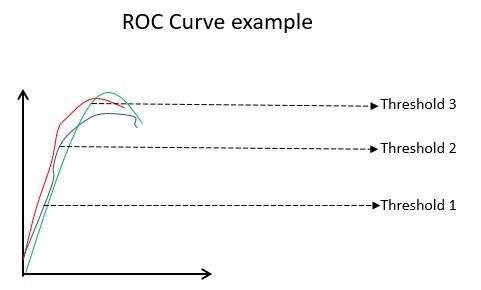
La courbe ROC (Receiver Operating Characteristic) illustre visuellement les performances d’un modèle de classification binaire pour différents seuils de classification. Il s’agit d’un graphique du TVP (Taux de Vrais Positifs) en fonction du TFP (Taux de Faux Positifs), calculé comme (1-Spécificité) pour différentes valeurs de seuil. La valeur la plus proche de 45 degrés (en haut à gauche) est la valeur de seuil la plus précise. Si le seuil est trop élevé, nous n’aurons pas beaucoup de faux positifs, mais plus de faux négatifs, et vice versa.
Généralement, lorsqu’on trace la courbe ROC de différents modèles, celui qui a la plus grande aire sous la courbe (AUC) est considéré comme le meilleur modèle.
Calculons toutes les valeurs métriques pour nos matrices de confusion Classificateur I et Classificateur II :
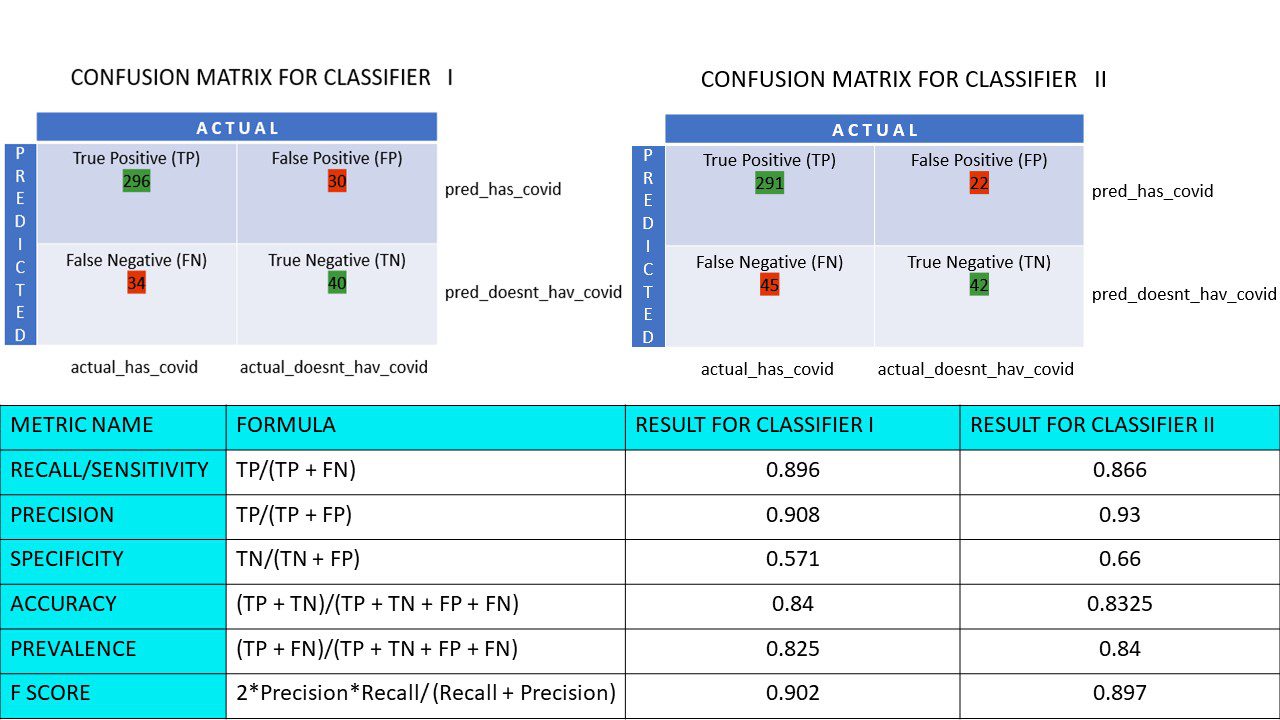
Nous observons que la justesse est plus élevée pour le classificateur II, tandis que la précision est légèrement supérieure pour le classificateur I. Les décideurs choisiront le classificateur I ou II en fonction du problème à résoudre.
Matrice de confusion N x N
Jusqu’à présent, nous avons abordé une matrice de confusion pour les classificateurs binaires. Qu’en est-il lorsqu’il y a plus de catégories que simplement oui/non ou aimer/ne pas aimer ? Par exemple, si votre algorithme doit trier des images selon qu’elles sont rouges, vertes ou bleues. Ce type de classification est appelé classification multiclasse. Le nombre de variables de sortie détermine la taille de la matrice. Dans ce cas, la matrice de confusion sera 3×3.

Sommaire
Une matrice de confusion est un excellent outil d’évaluation, car elle fournit des informations détaillées sur les performances d’un algorithme de classification. Elle est performante pour les classificateurs binaires et multiclasses, où il y a plus de deux paramètres à prendre en compte. Il est facile de visualiser une matrice de confusion, et nous pouvons générer toutes les autres mesures de performances, telles que le score F, la précision, le ROC et la justesse à l’aide de cette matrice.
Vous pouvez également découvrir comment choisir des algorithmes d’apprentissage automatique pour les problèmes de régression.