La mise en œuvre de la recherche est toujours difficile mais pas impossible.
Dans la vraie vie, nous ne rechercherons aucun modèle. Nous allons simplement aux endroits où nous pensons qu’il pourrait être placé. Nous ne suivons aucun modèle dans la plupart des cas.
Est-ce que la même chose fonctionne dans le monde de la programmation ?
Non! il doit y avoir un modèle pour rechercher des choses dans les programmes. Nous allons voir quelques algorithmes qui suivent différents modèles de recherche dans cet article.
Il existe plusieurs algorithmes que nous pouvons trouver dans le monde de la programmation. Nous allons discuter des algorithmes les plus importants et les plus utilisés dans cet article. Et le reste des algorithmes sera un jeu d’enfant à apprendre.
La recherche fait référence à la recherche d’un élément dans le tableau de cet article.
Voyons-les un par un.
Table des matières
Recherche linéaire
Le nom suggère que l’algorithme de recherche linéaire suit le modèle linéaire pour rechercher les éléments dans un tableau. L’algorithme commence à rechercher l’élément depuis le début du tableau et se déplace jusqu’à la fin jusqu’à ce qu’il trouve l’élément. Il arrête l’exécution du programme lorsqu’il trouve l’élément recherché.
Illustrons les algorithmes de recherche linéaire avec quelques illustrations intéressantes pour une meilleure compréhension de l’algorithme.
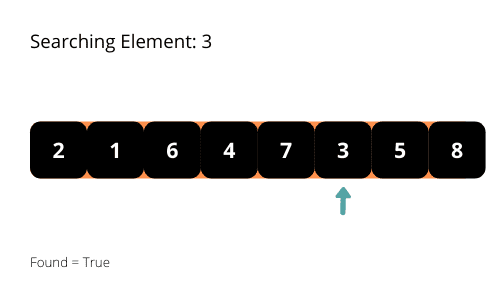
Si vous observez attentivement le modèle de recherche, vous constaterez que le temps nécessaire à l’exécution du programme prendra O(n) dans le pire des cas. Nous devons considérer la complexité temporelle dans le pire des cas des algorithmes à analyser. La complexité temporelle de l’algorithme est donc O(n).
Voyons l’implémentation de l’algorithme de recherche linéaire.
Implémentation de la recherche linéaire
Maintenant, vous avez une bonne compréhension de l’algorithme de recherche linéaire. Il est temps de se salir les mains avec du code. Voyons d’abord les étapes pour implémenter la recherche linéaire. Ensuite, vous essayez de le coder. Ne vous inquiétez pas même si vous ne pouvez pas; Je vous fournirai le code par la suite.
Voyons les étapes pour implémenter l’algorithme de recherche linéaire.
- Initialisez un tableau d’éléments (vos numéros porte-bonheur).
- Écrivez une fonction appelée search_element, qui accepte trois arguments, un tableau, la longueur du tableau et l’élément à rechercher.
- search_element(arr, n, element):
- Itérer sur le tableau donné.
- Vérifiez si l’élément actuel est égal à l’élément requis.
- Si oui, retournez True.
- Après avoir terminé la boucle, si l’exécution est toujours dans la fonction, l’élément n’est pas présent dans le tableau. Renvoie donc Faux.
- Itérer sur le tableau donné.
- Affiche le message en fonction de la valeur de retour de la fonction search_element.
Enfin, écrivez le code à l’aide des étapes ci-dessus pour implémenter l’algorithme de recherche linéaire.
Avez-vous terminé l’implémentation de l’algorithme de recherche linéaire ? Je l’espère. Si vous avez terminé, recoupez avec le code suivant.
Si vous ne l’avez pas terminé, ne vous inquiétez pas ; voir le code ci-dessous et découvrez comment nous l’avons implémenté. Vous l’obtiendrez sans trop d’effort.
## searching function def search_element(arr, n, element): ## iterating through the array for i in range(n): ## checking the current element with required element if arr[i] == element: ## returning True on match return True ## element is not found hence the execution comes here return False if __name__ == '__main__': ## initializing the array, length, and element to be searched arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] n = 10 element_to_be_searched = 6 # element_to_be_searched = 11 if search_element(arr, n, element_to_be_searched): print(element_to_be_searched, "is found") else: print(element_to_be_searched, "is not found")
Tout d’abord, exécutez le programme avec un élément présent dans le tableau. Et ensuite, exécutez-le avec un élément qui n’est pas présent dans le tableau.
La complexité temporelle de l’algorithme de recherche linéaire est O(n).
Pouvons-nous le réduire un peu plus avec des motifs différents ?
Oui, nous pouvons. Voyons ça.
Recherche binaire
L’algorithme de recherche binaire vérifie toujours l’élément du milieu du tableau. Cet algorithme recherche l’élément dans un tableau trié.
L’algorithme de recherche binaire parcourt le tableau et vérifie l’élément du milieu, s’il est trouvé, puis arrête le programme. Sinon, si l’élément du milieu est inférieur à l’élément requis, il omet la partie gauche du tableau de l’élément du milieu de la recherche. Sinon, si l’élément du milieu est supérieur à l’élément requis, il omet la partie droite du tableau de l’élément du milieu de la recherche.
A chaque itération, l’algorithme de recherche binaire réduit la zone pour rechercher l’élément. Ainsi, le nombre de vérifications est inférieur au nombre de vérifications effectuées dans l’algorithme de recherche linéaire.
Les illustrations nous aident à mieux comprendre l’algorithme de recherche binaire. Vérifions-les.
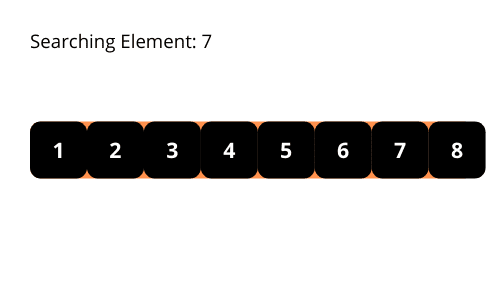
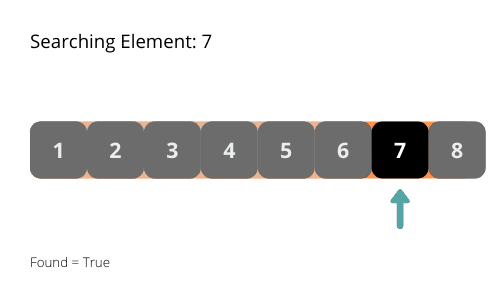
La complexité temporelle de l’algorithme de recherche binaire est O(log n). A chaque itération, la longueur de la zone de recherche se réduit de moitié. Il diminue de façon exponentielle.
Implémentation de la recherche binaire
Dans un premier temps, nous verrons les étapes pour implémenter l’algorithme de recherche binaire puis le code. Voyons les étapes pour terminer l’implémentation de l’algorithme de recherche binaire.
- Initialisez le tableau avec des éléments (vos numéros porte-bonheur)
- Écrivez une fonction appelée search_element, qui accepte trois arguments, un tableau trié, la longueur du tableau et l’élément à rechercher.
- search_element(sorted_arr, n, element):
- Initialisez la variable d’index i pour l’itération du tableau.
- Ensuite, initialisez deux variables pour maintenir la zone de recherche du tableau. Ici, nous les appelons début et fin car ils indiquent des index.
- Itérer jusqu’à ce que le i soit inférieur à la longueur du tableau.
- Calculez l’index du milieu de la zone de recherche à l’aide des valeurs de début et de fin. Ce sera (début + fin) // 2.
- Vérifiez si l’élément indexé du milieu de la zone de recherche est égal à l’élément requis ou non.
- Si oui, retournez True.
- Sinon, si l’élément indexé du milieu est inférieur à l’élément requis, déplacez l’index de début de la zone de recherche vers milieu + 1.
- Sinon, si l’élément indexé du milieu est supérieur à l’élément requis, déplacez l’index de fin de la zone de recherche vers le milieu – 1.
- Incrémenter l’indice du tableau i.
- Après avoir terminé la boucle, si l’exécution est toujours dans la fonction, l’élément n’est pas présent dans le tableau. Renvoie donc Faux.
- Affiche le message en fonction de la valeur de retour de la fonction search_element.
Essayez d’écrire le code similaire à l’implémentation de l’algorithme de recherche linéaire.
…
Avez-vous obtenu le code ?
Oui, comparez-le avec le code ci-dessous. Non, ne vous inquiétez pas; comprendre l’implémentation avec le code ci-dessous.
## searching function def search_element(sorted_arr, n, element): ## array index for iteration i = 0 ## variables to track the search area ## initializing them with start and end indexes start = 0 end = n - 1 ## iterating over the array while i < n: ## getting the index of the middle element middle = (start + end) // 2 ## checking the middle element with required element if sorted_arr[middle] == element: ## returning True since the element is in the array return True elif sorted_arr[middle] < element: ## moving the start index of the search area to right start = middle + 1 else: ## moving the end index of the search area to left end = middle - 1 i += 1 return False if __name__ == '__main__': ## initializing the array, length, and element to be searched arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] n = 10 element_to_be_searched = 9 # element_to_be_searched = 11 if search_element(arr, n, element_to_be_searched): print(element_to_be_searched, "is found") else: print(element_to_be_searched, "is not found")
Testez le code avec différents cas où l’élément est présent et non présent dans certains cas.
Conclusion
L’algorithme de recherche binaire est beaucoup plus efficace que l’algorithme de recherche linéaire. Nous devons trier le tableau car l’algorithme de recherche binaire n’est pas le cas dans l’algorithme de recherche linéaire. Le tri prend du temps. Mais, l’utilisation d’algorithmes efficaces pour le tri formera une bonne combinaison avec l’algorithme de recherche binaire.
Maintenant, vous avez une bonne connaissance des algorithmes les plus utilisés en Python.
Ensuite, découvrez quelques-uns des logiciels de recherche auto-hébergés les plus populaires.
Bon codage 🙂 🧑💻

