En Python, le type de données float est fréquemment employé pour représenter des nombres décimaux, également appelés nombres à virgule flottante. Ces nombres, positifs ou négatifs, se caractérisent par la présence d’une partie fractionnaire. La notation scientifique est également supportée, avec l’emploi de la lettre « e » ou « E » pour exprimer une puissance de 10.
Le type float est essentiel car il permet de manipuler une large gamme de nombres réels, qu’ils soient très petits ou très grands.
Voici quelques exemples de nombres de type float en Python :
# Exemples de nombres flottants a = 20.0 b = -51.51345 c = 65e7 d = -1.08E12 e = 2E10 print(type(a)) print(type(b)) print(type(c)) print(type(d)) print(type(e))
Résultat :
<class 'float'> <class 'float'> <class 'float'> <class 'float'> <class 'float'>
Comparés aux types de données comme les entiers, qui tronquent la partie décimale, les nombres à virgule flottante autorisent des calculs d’une plus grande exactitude. Ainsi, 3.142 serait réduit à 3 avec un entier, tandis qu’un float conserverait la valeur 3.142. Ils sont donc préférables pour des calculs mathématiques nécessitant précision.
Les float sont largement utilisés dans divers domaines tels que la modélisation, l’apprentissage automatique, la science des données, la finance, l’analyse économique, les graphiques, les visualisations, ainsi que les calculs scientifiques et techniques.
Entiers versus Flottants en Python
Les entiers, désignés par le type int en Python, constituent une autre catégorie de données courante. À la différence des float, ils sont dépourvus de partie décimale. Les entiers englobent les nombres positifs, négatifs et zéro.
Les entiers sont particulièrement utiles pour les opérations impliquant des nombres entiers, comme le comptage ou l’indexation.
Voici quelques exemples d’entiers :
a = 0 b = 968 c = -14 print(type(a)) print(type(b)) print(type(c))
Résultat :
<class 'int'> <class 'int'> <class 'int'>
Voici un tableau récapitulatif des principales différences entre les entiers et les nombres à virgule flottante :
| Caractéristique | Entiers (int) | Nombres à virgule flottante (float) |
| Représentent | Les nombres entiers, positifs, négatifs et zéro, sans partie décimale. | Les nombres réels avec une partie décimale. |
| Précision | Précision illimitée, la taille d’un entier n’est limitée que par la mémoire disponible. | Précision limitée, la plus grande valeur stockable est d’environ 1.8 x 10308. |
| Utilisation de la mémoire | Utilise moins de mémoire. | Utilise plus de mémoire. |
| Opérations au niveau du bit | Largement utilisés dans les opérations de manipulation de bits. | Rarement utilisés dans ce contexte. |
| Usage | Pour le comptage, l’indexation et la manipulation de bits. | Pour les mesures, les calculs scientifiques et la plupart des calculs mathématiques. |
Différentes Méthodes pour Créer et Manipuler des Flottants en Python
La méthode la plus directe pour travailler avec des float est d’assigner directement une valeur décimale à une variable, comme ceci :
# Assignation d'une valeur float à une variable a = 3.142
Il est également possible de convertir des entiers ou des chaînes de caractères numériques en valeurs float en utilisant le constructeur float(). Lorsque l’on passe un entier ou une chaîne numérique à float(), cela produit une valeur flottante correspondante :
number1 = 2524 numString1 = "513.523" numString2 = "1341" # Conversion en float et stockage dans une variable a = float(number1) print(a) b = float(numString1); print(b) c = float(numString2) print(c)
Résultat :
2524.0 513.523 1341.0
Dans l’exemple ci-dessus, les entiers et les chaînes sont convertis en float via float(). La valeur obtenue est ensuite stockée dans une variable et affichée.
Une autre façon d’obtenir des float est d’effectuer des opérations mathématiques telles que la division :
num1 = 20
num2 = 3
result = num1/num2
print("Résultat de la division en tant qu'entier :")
print(int(20/3))
print("Résultat de la division en tant que valeur flottante :")
print(result)
print(type(result))
Résultat :
Résultat de la division en tant qu'entier : 6 Résultat de la division en tant que valeur flottante : 6.666666666666667 <class 'float'>
Il est important de noter que la version float de la division offre une réponse plus précise que sa version entière.
Lors de la manipulation de nombres à virgule flottante, il est crucial de savoir comment ils sont représentés en interne dans un ordinateur. Les float sont stockés comme des fractions binaires (base 2). Or, la plupart des fractions décimales, notamment celles avec des décimales récurrentes, ne peuvent être représentées parfaitement en binaire. Par conséquent, les float sont souvent stockés comme des approximations.
Par exemple, la valeur 0.3 n’est pas stockée exactement comme 0.3. Pour visualiser cela, utilisons la fonction format() qui permet d’afficher un nombre avec un certain nombre de chiffres significatifs. Nous allons afficher 0.3 avec 20 chiffres significatifs :
num = 0.3
print("num avec 20 chiffres significatifs")
print(format(num, '.20f'))
print("La valeur de num stockée")
print(num)
Résultat:
num avec 20 chiffres significatifs 0.29999999999999998890 La valeur de num stockée 0.3
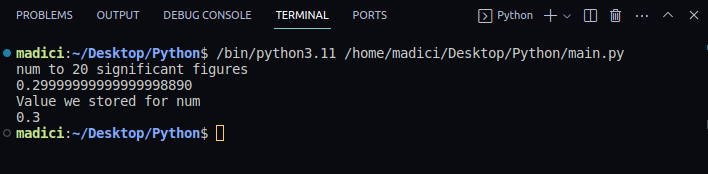
La valeur 0.3 n’est pas stockée précisément comme 0.3 en interne, mais plutôt comme une approximation. C’est pourquoi l’impression de la variable num donne une valeur arrondie.
Cette imprécision peut entraîner des résultats inattendus. Par exemple, 0.3 + 0.3 + 0.3 devrait donner 0.9. Pourtant, Python stockant des approximations de fractions binaires, le résultat peut être différent :
sum = 0.3 + 0.3 + 0.3
answer = 0.9
print("La somme est-elle égale à la réponse ?")
print(sum == answer)
print("La représentation interne de la somme est :")
print(sum)
print("La réponse du calcul manuel est :")
print(answer)
Résultat :
La somme est-elle égale à la réponse ? False La représentation interne de la somme est : 0.8999999999999999 La réponse du calcul manuel est : 0.9
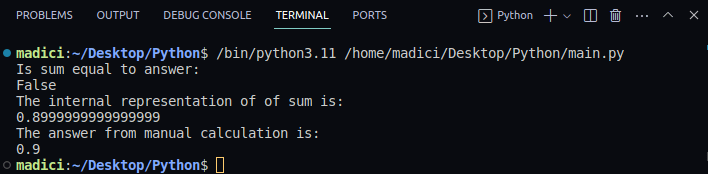
Il est crucial de comprendre que Python manipule des approximations des valeurs réelles. Lors de comparaisons, il est souvent nécessaire d’arrondir les nombres avant de vérifier l’égalité. Pour une meilleure précision avec les float, il est recommandé d’utiliser le module decimal intégré.
Le Module decimal en Python
Dans les situations où une grande précision est primordiale, le type float peut ne pas être optimal. Le module decimal est conçu pour garantir une précision accrue dans les calculs financiers ou scientifiques.
Contrairement au type float, qui est stocké sous forme de représentations binaires dépendantes de la machine, le module decimal utilise une représentation décimale indépendante de la machine, assurant une plus grande précision. Il permet de représenter les nombres décimaux avec exactitude et d’effectuer des calculs en conséquence, offrant une arithmétique décimale avec un arrondi précis.
Pour utiliser le module decimal, importez-le dans votre script Python :
import decimal
Pour voir l’intérêt du module decimal, reprenons la comparaison précédente avec 0.3 + 0.3 + 0.3 et 0.9 :
import decimal
sum = decimal.Decimal('0.3') + decimal.Decimal('0.3') + decimal.Decimal('0.3')
answer = decimal.Decimal('0.9')
print("La somme est-elle égale à la réponse ?")
print(sum == answer)
print("La représentation interne de la somme est :")
print(sum)
print("La réponse du calcul manuel est :")
print(answer)
Résultat :
La somme est-elle égale à la réponse ? True La représentation interne de la somme est : 0.9 La réponse du calcul manuel est : 0.9
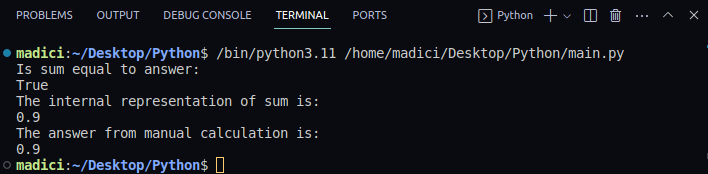
Avec le module decimal, la comparaison donne un résultat exact et précis. Par conséquent, pour une précision accrue, privilégiez ce module lors de vos calculs avec des nombres à virgule flottante.
Erreurs Fréquentes lors de l’Utilisation des Flottants
La majorité des erreurs rencontrées avec les float en Python résultent d’une mauvaise compréhension de leur représentation interne. Les valeurs telles que 0.3 ne sont pas stockées précisément comme 0.3, ce qui peut conduire à des erreurs si l’on suppose le contraire.

Une erreur courante est l’erreur d’arrondi qui peut survenir lors de calculs mathématiques. Puisque les float sont stockés comme des approximations, les résultats peuvent différer de ce que l’on attend.
Ces erreurs d’arrondi peuvent poser problème lors de comparaisons d’égalité. La prudence est donc de mise et il est crucial d’être conscient des potentiels résultats inattendus.
L’utilisation du module decimal permet de contourner la plupart de ces erreurs en offrant une précision accrue et en assurant des résultats plus prévisibles et exacts.
Conclusion
En tant que développeur Python, vous serez amené à travailler régulièrement avec le type de données float. Pour éviter des erreurs, il est important de comprendre sa représentation interne. Il est crucial d’éviter les comparaisons d’égalité directe car Python manipule des approximations des nombres à virgule flottante.
Pour des applications nécessitant une grande précision, évitez d’utiliser les float et préférez le module decimal, qui permet de représenter et de manipuler ces nombres avec une exactitude accrue et de façon indépendante de la machine.
Vous pouvez également explorer les fonctionnalités des fonctions Python Itertools et la gestion d’exceptions avec Python Try Except.