Le processus de classement est une opération fondamentale en programmation, et l’efficacité de cette opération dépend grandement de l’algorithme utilisé. Un choix inadéquat peut entraîner des temps d’exécution excessivement longs.
Cet article explore divers algorithmes de tri, en détaillant leurs principes de fonctionnement.
Nous allons examiner pas à pas différents algorithmes de tri. Bien que l’implémentation soit présentée en Python, la logique sous-jacente peut être facilement adaptée à d’autres langages. L’adaptation se résume à une question de syntaxe spécifique au langage.
Nous aborderons les algorithmes en commençant par les moins performants pour finir avec les plus efficaces. Ne vous inquiétez pas, suivez attentivement l’article et essayez de les mettre en œuvre par vous-même.
Entrons maintenant dans le vif du sujet et explorons ces algorithmes de tri.
Tri par insertion
Le tri par insertion se distingue par sa simplicité et sa facilité de mise en œuvre. Cependant, son efficacité diminue pour les tableaux de grande taille, ce qui limite son utilisation dans ces cas.
Cet algorithme maintient deux parties distinctes au sein du tableau : une partie triée et une partie non triée.
Au début du processus, la partie triée ne contient que le premier élément du tableau. L’algorithme consiste à sélectionner un élément de la partie non triée et à l’insérer à sa place appropriée dans la partie triée.
Pour une meilleure compréhension, examinons les étapes de cet algorithme à l’aide d’un exemple visuel.
Voici les étapes détaillées pour implémenter le tri par insertion :
- Initialisez un tableau avec des valeurs numériques arbitraires.
- Parcourez le tableau à partir du deuxième élément.
- Stockez la position et la valeur de l’élément actuel dans des variables.
- Exécutez une boucle qui continue tant que la position est valide et que l’élément actuel est inférieur à l’élément précédent.
- Déplacez l’élément précédent à la position de l’élément actuel.
- Décrémentez la position actuelle.
- Une fois la boucle terminée (soit au début du tableau, soit en trouvant un élément plus petit), insérez l’élément actuel à la position correcte.
La complexité temporelle du tri par insertion est de O(n^2), tandis que sa complexité spatiale est de O(1).
Voilà, le tableau est maintenant trié. Le code suivant illustre l’implémentation en Python. Assurez-vous d’avoir Python installé ou utilisez un compilateur en ligne.
def insertion_sort(arr, n):
for i in range(1, n):
# Position et élément courants
current_position = i
current_element = arr[i]
# Itération tant que
# la position est valide et que l'élément actuel est plus petit que le précédent
while current_position > 0 and current_element < arr[current_position - 1]:
# Déplacement de l'élément précédent à la position actuelle
arr[current_position] = arr[current_position - 1]
# Déplacement à la position précédente
current_position -= 1
# Insertion de l'élément à la position correcte
arr[current_position] = current_element
if __name__ == '__main__':
# Initialisation du tableau
arr = [3, 4, 7, 8, 1, 9, 5, 2, 6]
insertion_sort(arr, 9)
# Affichage du tableau trié
print(str(arr))
Tri par sélection
Le tri par sélection présente des similitudes avec le tri par insertion. L’algorithme divise le tableau en deux parties, une triée et une non triée. À chaque itération, il recherche l’élément minimum dans la partie non triée et le place à la fin de la partie triée.
Examinons visuellement les étapes du tri par sélection pour une meilleure compréhension.
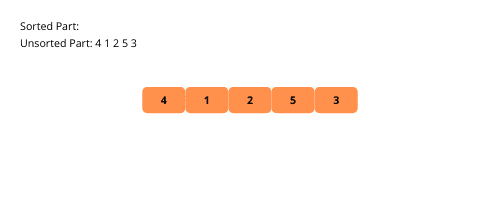
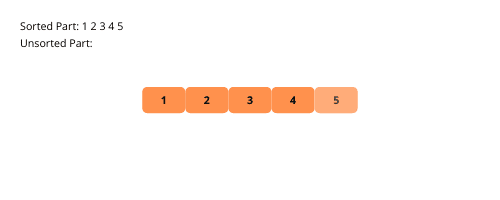
Voici les étapes pour implémenter le tri par sélection :
- Initialisez un tableau avec des valeurs numériques.
- Parcourez le tableau.
- Mémorisez l’indice de l’élément minimum.
- Parcourez le tableau, en partant de l’élément actuel jusqu’à la fin.
- Vérifiez si l’élément actuel est inférieur à l’élément minimum.
- Si c’est le cas, mettez à jour l’indice de l’élément minimum.
- Échangez l’élément actuel avec l’élément minimum trouvé.
La complexité temporelle du tri par sélection est O(n^2), et sa complexité spatiale est O(1).
Tentez d’implémenter l’algorithme. Il est similaire au tri par insertion. Vous pouvez consulter le code ci-dessous.
def selection_sort(arr, n):
for i in range(n):
# Mémorisation de l'indice de l'élément minimum
min_element_index = i
for j in range(i + 1, n):
# Recherche de l'indice de l'élément minimum
if arr[j] < arr[min_element_index]:
min_element_index = j
# Échange de l'élément actuel avec l'élément minimum
arr[i], arr[min_element_index] = arr[min_element_index], arr[i]
if __name__ == '__main__':
# Initialisation du tableau
arr = [3, 4, 7, 8, 1, 9, 5, 2, 6]
selection_sort(arr, 9)
# Affichage du tableau trié
print(str(arr))
Tri à bulles
Le tri à bulles est un algorithme simple qui consiste à comparer et à permuter les éléments adjacents à plusieurs reprises jusqu’à ce que le tableau soit entièrement trié.
L’algorithme parcourt le tableau et déplace l’élément courant vers sa position suivante tant qu’il est supérieur à l’élément qui le suit.
Visualisons le tri à bulles pour faciliter la compréhension.
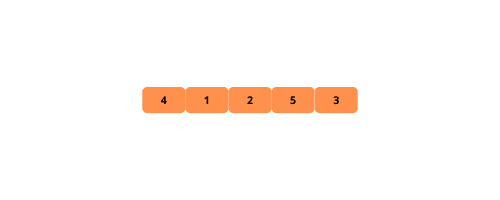
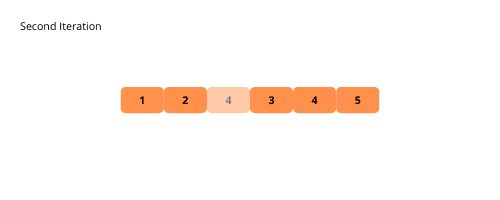
Voici les étapes pour implémenter le tri à bulles :
- Initialisez le tableau avec des données factices.
- Parcourez le tableau.
- Parcourez le tableau de 0 à n-i-1 (car les i derniers éléments sont déjà triés).
- Comparez l’élément actuel avec l’élément suivant.
- Si l’élément actuel est supérieur à l’élément suivant, échangez-les.
La complexité temporelle du tri à bulles est O(n^2), avec une complexité spatiale de O(1).
Vous pouvez maintenant implémenter facilement le tri à bulles. Voici le code :
def bubble_sort(arr, n):
for i in range(n):
# Parcours du tableau jusqu'à n-i-1
for j in range(n - i - 1):
# Comparaison avec l'élément suivant
if arr[j] > arr[j + 1]:
# Échange des éléments adjacents
arr[j], arr[j + 1] = arr[j + 1], arr[j]
if __name__ == '__main__':
# Initialisation du tableau
arr = [3, 4, 7, 8, 1, 9, 5, 2, 6]
bubble_sort(arr, 9)
# Affichage du tableau trié
print(str(arr))
Tri par fusion
Le tri par fusion est un algorithme récursif qui utilise une approche diviser pour mieux régner. Il est plus performant que les algorithmes précédents en termes de complexité temporelle.
L’algorithme consiste à diviser le tableau en deux moitiés, à les trier séparément, puis à les fusionner en un seul tableau trié.
Étant donné qu’il s’agit d’un algorithme récursif, le processus de division se poursuit jusqu’à ce que le tableau soit réduit à des sous-tableaux unitaires, qui sont trivialement triés.
Passons à une représentation visuelle de ce processus.
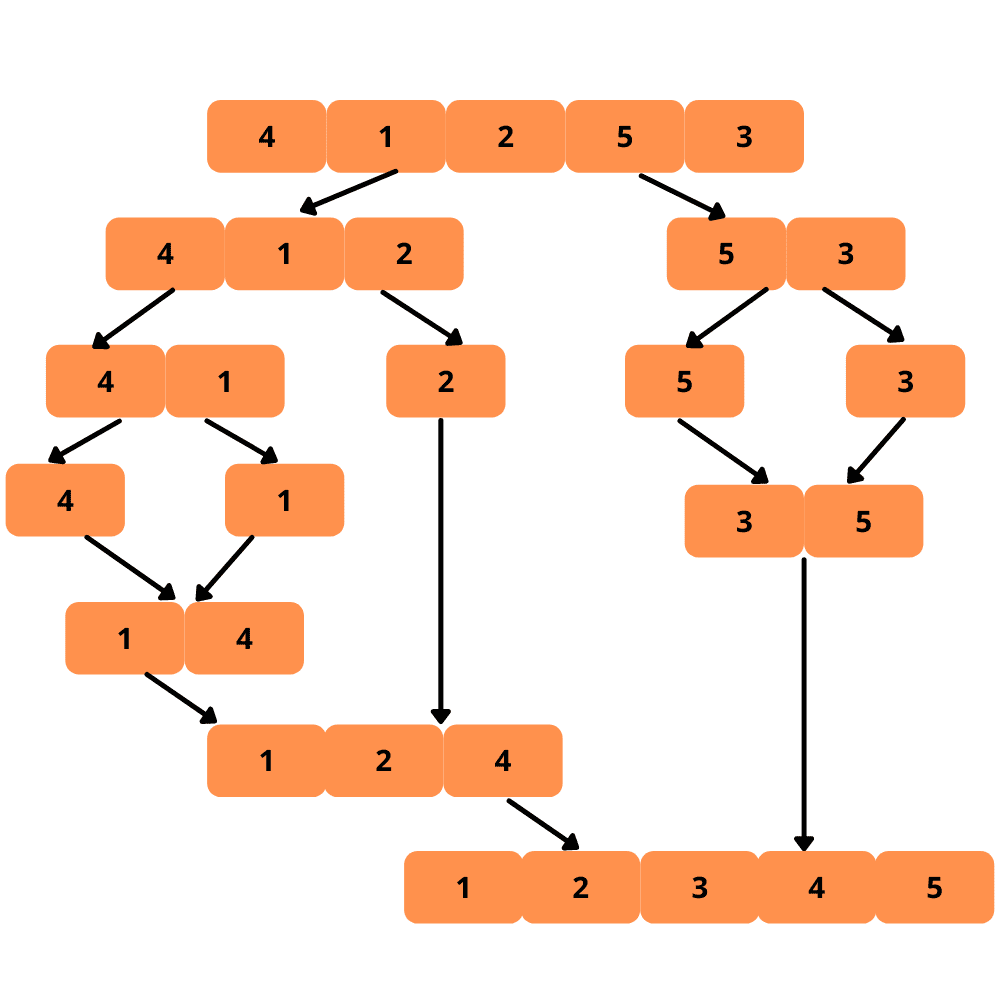
Voici les étapes pour mettre en œuvre le tri par fusion :
- Initialisez un tableau avec des données factices (des entiers).
- Définissez une fonction `merge` pour fusionner deux sous-tableaux en un tableau trié. Elle prend en arguments : le tableau, l’indice de début, l’indice du milieu et l’indice de fin.
- Calculez les longueurs des deux sous-tableaux en utilisant les indices fournis.
- Copiez les éléments du tableau dans les tableaux gauche et droit respectivement.
- Parcourez les deux sous-tableaux.
- Comparez les éléments des deux sous-tableaux.
- Incorporez l’élément le plus petit des deux sous-tableaux au tableau fusionné.
- Vérifiez s’il reste des éléments dans les deux sous-tableaux et ajoutez-les.
- Définissez une fonction `merge_sort` avec le tableau, les indices gauche et droit comme paramètres.
- Si l’indice de gauche est supérieur ou égal à l’indice de droite, arrêtez la récursion.
- Trouvez l’indice du milieu pour diviser le tableau en deux moitiés.
- Appelez récursivement `merge_sort` sur les deux moitiés du tableau.
- Après les appels récursifs, fusionnez les deux moitiés en utilisant la fonction `merge`.
La complexité temporelle du tri par fusion est O(n log n), et sa complexité spatiale est O(n).
C’est tout pour l’implémentation de l’algorithme de tri par fusion. Voici le code :
def merge(arr, left_index, mid_index, right_index):
# Création des sous-tableaux gauche et droit
left_array = arr[left_index:mid_index+1]
right_array = arr[mid_index+1:right_index+1]
# Calcul des longueurs des sous-tableaux
left_array_length = mid_index - left_index + 1
right_array_length = right_index - mid_index
# Indices pour fusionner les deux tableaux
i = j = 0
# Indice pour le remplacement des éléments dans le tableau
k = left_index
# Parcours des deux sous-tableaux
while i < left_array_length and j < right_array_length:
# Comparaison des éléments
if left_array[i] < right_array[j]:
arr[k] = left_array[i]
i += 1
else:
arr[k] = right_array[j]
j += 1
k += 1
# Ajout des éléments restants
while i < left_array_length:
arr[k] = left_array[i]
i += 1
k += 1
while j < right_array_length:
j += 1
k += 1
def merge_sort(arr, left_index, right_index):
# Condition de base pour la récursion
if left_index >= right_index:
return
# Calcul de l'indice du milieu
mid_index = (left_index + right_index) // 2
# Appels récursifs
merge_sort(arr, left_index, mid_index)
merge_sort(arr, mid_index + 1, right_index)
# Fusion des deux sous-tableaux
merge(arr, left_index, mid_index, right_index)
if __name__ == '__main__':
# Initialisation du tableau
arr = [3, 4, 7, 8, 1, 9, 5, 2, 6]
merge_sort(arr, 0, 8)
# Affichage du tableau trié
print(str(arr))
Conclusion
Il existe une multitude d’autres algorithmes de tri, mais ceux présentés ici sont parmi les plus couramment utilisés. J’espère que vous avez apprécié cette exploration du tri.
Pour la suite, nous aborderons les algorithmes de recherche.
Bon codage 🙂 👨💻