Dans le domaine de l’analyse des données, une valeur aberrante représente une observation qui s’écarte de manière significative des autres valeurs dans un ensemble de données. Ces valeurs atypiques peuvent avoir un impact considérable sur les résultats, notamment lors de l’utilisation d’outils comme Excel. En effet, elles peuvent biaiser les calculs de moyenne, rendant l’interprétation des données plus difficile. Heureusement, Excel propose diverses fonctions qui permettent d’identifier et de gérer ces valeurs aberrantes de manière efficace.
Détection Rapide d’Anomalies : Un Exemple Concret
Imaginez un ensemble de données où l’on observe des valeurs telles que 2 et 173. Ces chiffres se distinguent nettement des autres et sont facilement identifiables comme des valeurs aberrantes. Dans ce type de jeu de données simple, il est possible de les traiter manuellement. Cependant, cette approche devient impraticable lorsque l’on travaille avec des ensembles de données plus vastes. Il est donc essentiel de maîtriser les techniques d’identification et de suppression des valeurs aberrantes afin d’obtenir des analyses statistiques précises.
Dans cet article, nous allons explorer différentes méthodes pour identifier ces valeurs atypiques et les exclure des calculs statistiques, en utilisant les fonctionnalités d’Excel.
Méthodologie pour Localiser les Valeurs Aberrantes
La localisation des valeurs aberrantes nécessite une approche structurée, comprenant les étapes suivantes :
- Calcul des premier et troisième quartiles (nous allons expliquer ce que cela signifie).
- Détermination de l’étendue interquartile (plus de détails suivront).
- Calcul des limites supérieure et inférieure de l’ensemble de données.
- Identification des points de données situés en dehors de ces limites.
Nous allons utiliser une zone spécifique de la feuille de calcul pour stocker les résultats de nos calculs.
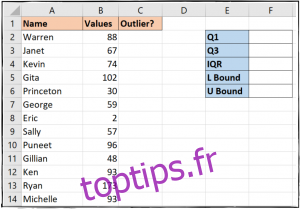
Commençons par la première étape.
Première Étape : Calcul des Quartiles
Lorsqu’un ensemble de données est divisé en quatre parties égales, chacune de ces parties est appelée un quartile. Le premier quartile (Q1) représente les 25% inférieurs des données, le deuxième quartile (Q2) correspond à la médiane, et ainsi de suite. Cette étape est essentielle, car la définition la plus courante d’une valeur aberrante est un point de données situé à plus de 1,5 fois l’étendue interquartile (IQR) en dessous de Q1 ou au-dessus de Q3. Pour identifier ces valeurs, il faut donc commencer par déterminer les quartiles.
Excel propose la fonction QUARTILE pour calculer ces valeurs. Cette fonction requiert deux arguments : la plage de données et le numéro du quartile souhaité.
=QUARTILE(plage, quartile)
La plage représente l’ensemble de valeurs à évaluer et le quartile est un nombre (1, 2 ou 3) correspondant au quartile souhaité.
Note : Depuis Excel 2010, les fonctions QUARTILE.INC et QUARTILE.EXC ont été introduites. La fonction QUARTILE reste cependant la plus polyvalente pour la compatibilité entre différentes versions d’Excel.
Revenons à notre exemple.

Pour calculer Q1, nous allons saisir la formule suivante en F2 :
=QUARTILE(B2:B14;1)
Excel propose une liste d’options pour l’argument du quartile.
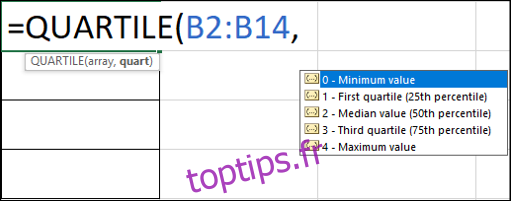
Pour calculer Q3, nous utilisons la même formule en F3 en remplaçant 1 par 3 :
=QUARTILE(B2:B14;3)
Nous avons maintenant les valeurs de Q1 et Q3 affichées dans nos cellules.
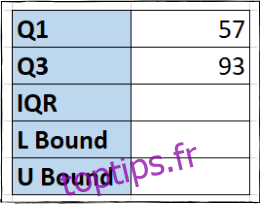
Deuxième Étape : Calcul de l’Étendue Interquartile
L’étendue interquartile (IQR) est l’étendue des 50 % centraux des données, calculée comme la différence entre Q3 et Q1.
En F4, nous allons saisir une formule qui soustrait Q1 de Q3 :
=F3-F2
L’IQR est désormais visible.
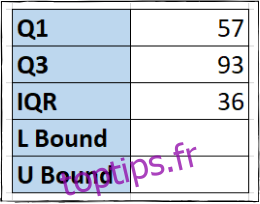
Troisième Étape : Définition des Limites Inférieure et Supérieure
Les limites inférieure et supérieure définissent l’intervalle de valeurs considérées comme acceptables. Toute valeur en dehors de cet intervalle est classée comme valeur aberrante.
En F5, nous allons calculer la limite inférieure en multipliant l’IQR par 1,5 et en la soustrayant de Q1 :
=F2-(1,5*F4)
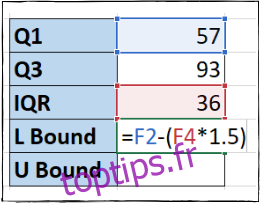
Les parenthèses ne sont pas strictement nécessaires, car la multiplication est prioritaire, mais elles facilitent la lecture de la formule.
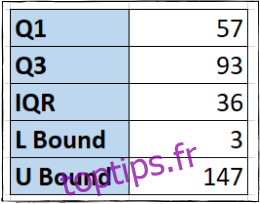
En F6, nous allons calculer la limite supérieure en multipliant l’IQR par 1,5 et en l’ajoutant à Q3 :
=F3+(1,5*F4)
Quatrième Étape : Identification des Valeurs Aberrantes
Avec tous les calculs préparatoires effectués, il est temps d’identifier les points de données qui sont en dehors de nos limites, c’est-à-dire les valeurs aberrantes. Pour cela, nous allons utiliser la fonction OU pour tester si une valeur est inférieure à la limite inférieure ou supérieure à la limite supérieure. Nous saisissons la formule suivante en C2 :
=OU(B2$F$6)
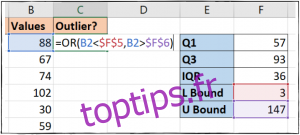
Nous allons ensuite copier cette formule dans les cellules C3 à C14. Si la valeur renvoyée est VRAI, cela signifie qu’il s’agit d’une valeur aberrante. Dans notre exemple, nous pouvons voir que deux valeurs sont considérées comme telles.
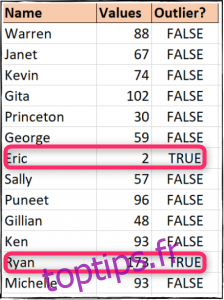
Calcul de Moyenne en Ignorant les Valeurs Aberrantes
Bien que la méthode basée sur les quartiles permette d’identifier les valeurs aberrantes, Excel offre une solution plus rapide pour calculer la moyenne sans tenir compte de ces valeurs atypiques : la fonction MOYENNE.REDUITE. Cette méthode ne permet pas d’identifier spécifiquement les valeurs aberrantes, mais elle donne la possibilité d’ajuster le seuil de données exclues.
La syntaxe de la fonction est la suivante :
=MOYENNE.REDUITE(plage; pourcentage)
La plage représente l’ensemble de données à moyenner et le pourcentage est la proportion de valeurs à exclure aux deux extrémités de l’ensemble de données (ce pourcentage peut être saisi sous forme décimale ou en pourcentage).
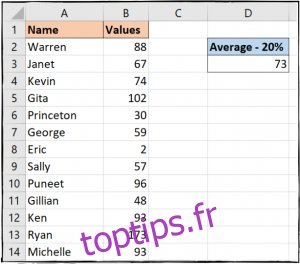
Dans notre exemple, nous allons saisir la formule suivante en D3 pour calculer la moyenne en excluant 20 % des valeurs :
=MOYENNE.REDUITE(B2:B14; 20%)
En résumé, Excel propose différentes fonctions pour gérer les valeurs aberrantes. Que vous souhaitiez les identifier pour des rapports spécifiques ou les exclure des calculs, Excel a la fonction appropriée à vos besoins.