Aide-mémoire Big O : expliqué avec des exemples Python

Table des matières

L’analyse Big O est une méthode d’évaluation et de classification de l’efficacité des algorithmes.

Elle permet de sélectionner les algorithmes les plus performants et adaptables. Cet article sert de pense-bête sur la notation Big O, abordant les points essentiels à connaître.

Qu’est-ce que l’analyse Big O ?

L’analyse Big O est une technique utilisée pour étudier l’évolution des performances d’un algorithme. Plus précisément, elle s’intéresse à l’efficacité d’un algorithme lorsque la taille de son entrée augmente.

L’efficacité se mesure à la manière dont les ressources du système sont utilisées pour obtenir un résultat. Les ressources principalement concernées sont le temps d’exécution et la mémoire utilisée.

Par conséquent, lors d’une analyse Big O, les questions posées sont les suivantes :

Comment l’utilisation de la mémoire par un algorithme varie-t-elle en fonction de la taille de l’entrée ?
Comment le temps nécessaire à un algorithme pour produire un résultat évolue-t-il avec l’augmentation de la taille de l’entrée ?

La réponse à la première question concerne la complexité spatiale de l’algorithme, tandis que la seconde porte sur sa complexité temporelle. La notation Big O est l’outil utilisé pour exprimer ces complexités. Nous approfondirons cela plus loin dans ce pense-bête.

Prérequis

Avant de poursuivre, il est important de noter que pour tirer le meilleur parti de ce pense-bête, une certaine familiarité avec l’algèbre est recommandée. De plus, comme des exemples en Python seront fournis, une connaissance de base de ce langage est également utile. Cependant, aucune compétence approfondie en programmation n’est requise, car aucun code ne sera à écrire.

Comment réaliser une analyse Big O

Cette section explore la manière dont une analyse Big O est effectuée.

Il est essentiel de se rappeler que les performances d’un algorithme sont liées à la structure des données d’entrée lors de l’analyse de la complexité Big O.

Par exemple, les algorithmes de tri sont plus rapides lorsque les données sont déjà ordonnées. Il s’agit du scénario idéal pour l’algorithme. Inversement, ces mêmes algorithmes sont plus lents si les données sont dans l’ordre inverse. C’est le pire scénario.

Lors d’une analyse Big O, seule la situation la plus défavorable est prise en compte.

Analyse de la complexité spatiale

Cette partie du pense-bête Big O examine comment évaluer la complexité spatiale. L’objectif est d’analyser l’évolution de la mémoire supplémentaire utilisée par un algorithme lorsque l’entrée augmente.

Prenons l’exemple d’une fonction utilisant la récursivité pour effectuer une boucle de n à zéro. Sa complexité spatiale est directement proportionnelle à n. En effet, plus n est grand, plus il y a d’appels de fonction sur la pile d’appels. Cela lui donne une complexité spatiale de O(n).

def loop_recursively(n):
    if n == -1:
        return
    else:
        print(n)
        loop_recursively(n - 1)

Une implémentation plus efficace serait la suivante :

def loop_normally(n):
    count = n
    while count >= 0:
        print(count)
        count =- 1

Dans cet algorithme, une seule variable supplémentaire est créée pour réaliser la boucle. Même si n augmentait considérablement, l’utilisation de la mémoire supplémentaire resterait constante. Par conséquent, l’algorithme a une complexité spatiale constante, notée O(1).

En comparant les complexités spatiales de ces deux algorithmes, la boucle `while` s’avère plus performante que la récursivité. C’est l’objectif fondamental de l’analyse Big O : évaluer comment les algorithmes évoluent en fonction de la taille des données d’entrée.

Analyse de la complexité temporelle

Dans l’analyse de la complexité temporelle, l’intérêt ne porte pas sur le temps d’exécution total, mais sur l’évolution du nombre d’opérations de calcul. Le temps réel peut varier en fonction de nombreux facteurs systémiques et aléatoires difficiles à quantifier. L’analyse se concentre donc sur l’évolution du nombre d’opérations, en considérant chaque opération comme équivalente.

Pour illustrer l’analyse de la complexité temporelle, prenons l’exemple suivant :

Supposons une liste d’utilisateurs, chacun ayant un identifiant et un nom. La tâche est d’implémenter une fonction qui, à partir d’un identifiant, renvoie le nom de l’utilisateur correspondant. Voici une solution possible :

users = [
    {'id': 0, 'name': 'Alice'},
    {'id': 1, 'name': 'Bob'},
    {'id': 2, 'name': 'Charlie'},
]

def get_username(id, users):
    for user in users:
        if user['id'] == id:
            return user['name']
    return 'User not found'

get_username(1, users)

Pour cette fonction, l’algorithme parcourt l’intégralité de la liste jusqu’à trouver l’utilisateur avec l’identifiant recherché. Avec trois utilisateurs, l’algorithme effectue trois itérations. Avec dix utilisateurs, il en effectue dix.

Le nombre d’opérations est donc directement proportionnel au nombre d’utilisateurs. L’algorithme a une complexité temporelle linéaire. Cependant, il est possible d’améliorer cet algorithme.

Imaginons que les utilisateurs ne soient pas stockés dans une liste, mais dans un dictionnaire. L’algorithme de recherche ressemblerait alors à ceci :

users = {
    '0': 'Alice',
    '1': 'Bob',
    '2': 'Charlie'
}

def get_username(id, users):
     if id in users:
         return users[id]
     else:
         return 'User not found'

get_username(1, users)

Avec ce nouvel algorithme, quel que soit le nombre d’utilisateurs, le nombre d’opérations nécessaires pour retrouver le nom d’utilisateur reste le même. L’algorithme a une complexité constante. La taille de l’entrée n’affecte pas le nombre d’étapes de calcul.

Qu’est-ce que la notation Big O ?

La section précédente expliquait comment évaluer la complexité spatiale et temporelle d’algorithmes à l’aide de l’analyse Big O. Des termes tels que « linéaire » et « constant » ont été utilisés pour décrire ces complexités. La notation Big O est un autre moyen de représenter ces complexités.

La notation Big O est une méthode pour exprimer les complexités spatiales et temporelles d’un algorithme. Sa forme est simple : un O suivi de parenthèses. Entre ces parenthèses, une fonction de n décrit la complexité spécifique.

Une complexité linéaire est représentée par n, et s’écrit donc O(n) (prononcé « O de n »). Une complexité constante est représentée par 1, et s’écrit O(1).

Il existe d’autres complexités, qui seront abordées dans la section suivante. En règle générale, pour déterminer la complexité d’un algorithme, les étapes suivantes sont à suivre :

Tenter de définir une fonction mathématique de n, f(n), où f(n) représente la quantité de mémoire utilisée ou le nombre d’opérations effectuées par l’algorithme, et n est la taille de l’entrée.
Identifier le terme dominant de cette fonction. L’ordre de dominance des termes, du plus dominant au moins dominant, est le suivant : factoriel, exponentiel, polynomial, quadratique, linéaire, logarithmique, et constant.
Supprimer tous les coefficients du terme dominant.

Le résultat de ces étapes est le terme placé entre parenthèses dans la notation Big O.

Exemple:

Considérons la fonction Python suivante :

users = [
    'Alice',
    'Bob',
    'Charlie'
]

def print_users(users):
    number_of_users = len(users)
    print("Total number of users:", number_of_users)

    for i in number_of_users:
        print(i, end=': ')
        print(user)

Nous allons calculer la complexité temporelle Big O de cet algorithme.

Tout d’abord, une fonction mathématique de n, f(n), est établie pour représenter le nombre d’opérations de calcul effectuées par l’algorithme. Rappelons que n représente la taille de l’entrée.

Dans notre code, la fonction effectue deux opérations : une pour calculer le nombre d’utilisateurs et une pour l’afficher. Ensuite, pour chaque utilisateur, elle effectue deux opérations : une pour afficher l’indice et une pour afficher le nom de l’utilisateur.

La fonction mathématique qui représente le mieux le nombre d’opérations effectuées est donc f(n) = 2 + 2n, où n est le nombre d’utilisateurs.

L’étape suivante consiste à sélectionner le terme dominant. 2n est un terme linéaire et 2 est un terme constant. Le terme linéaire est plus dominant que le terme constant, nous choisissons donc 2n.

Notre fonction devient donc f(n) = 2n.

Enfin, les coefficients sont supprimés. Dans notre fonction, 2 est le coefficient. Après suppression, la fonction devient f(n) = n. C’est ce terme qui sera utilisé dans la notation Big O.

Par conséquent, la complexité temporelle de notre algorithme est O(n), soit une complexité linéaire.

Les différentes complexités Big O

La dernière section de ce pense-bête présente les différentes complexités Big O et leurs représentations graphiques.

#1. Constante

Une complexité constante signifie que l’algorithme utilise une quantité fixe de mémoire (dans l’analyse de la complexité spatiale) ou effectue un nombre constant d’opérations (dans l’analyse de la complexité temporelle). C’est la complexité idéale, car l’algorithme n’a pas besoin de ressources supplémentaires à mesure que la taille de l’entrée augmente. Il est donc très évolutif.

La complexité constante est notée O(1). Cependant, il n’est pas toujours possible de créer des algorithmes avec une complexité constante.

#2. Logarithmique

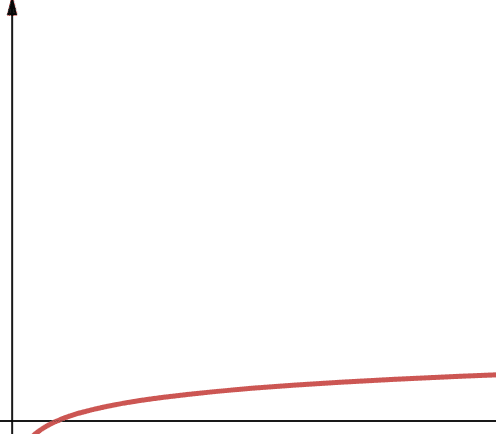
La complexité logarithmique est notée O(log n). Il est important de souligner que si la base du logarithme n’est pas spécifiée en informatique, elle est implicitement égale à 2.

Par conséquent, log n est équivalent à log₂n. Les fonctions logarithmiques ont une croissance rapide au début, qui ralentit par la suite. Elles sont efficaces et évolutives même avec de grandes valeurs de n.

#3. Linéaire

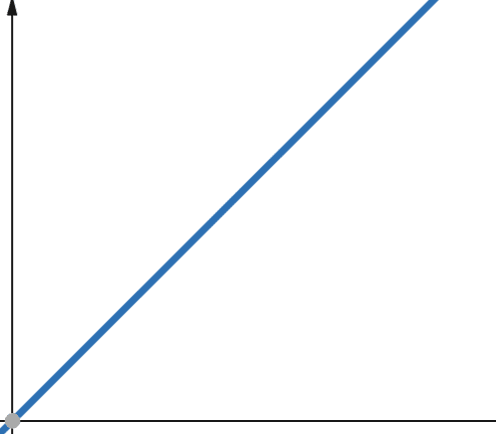
Dans le cas des fonctions linéaires, si la variable indépendante est multipliée par un facteur p, la variable dépendante est également multipliée par le même facteur p.

Par conséquent, une fonction avec une complexité linéaire augmente proportionnellement à la taille de l’entrée. Si la taille de l’entrée double, le nombre d’opérations ou l’utilisation de la mémoire double également. La complexité linéaire est notée O(n).

#4. Linéarithmique

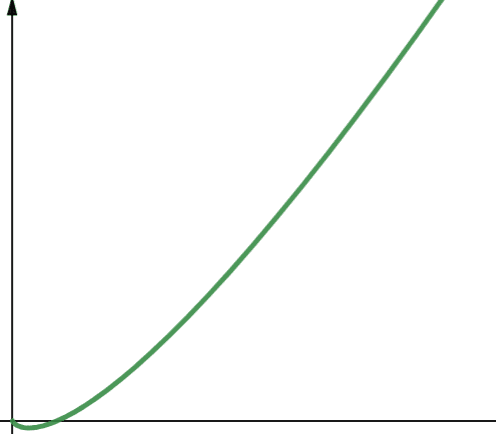
Les fonctions linéarithmiques sont notées O(n * log n). Il s’agit d’une fonction linéaire multipliée par une fonction logarithmique. Les fonctions linéarithmiques ont des performances légèrement supérieures aux fonctions linéaires lorsque log n est supérieur à 1. En effet, n est multiplié par un nombre supérieur à 1.

Log n est supérieur à 1 pour toutes les valeurs de n supérieures à 2 (car log n est log₂n). Par conséquent, pour toutes les valeurs de n supérieures à 2, les fonctions linéaires sont moins évolutives que les fonctions linéarithmiques. Comme n est généralement supérieur à 2, les fonctions linéaires sont généralement moins évolutives que les fonctions linéarithmiques.

#5. Quadratique

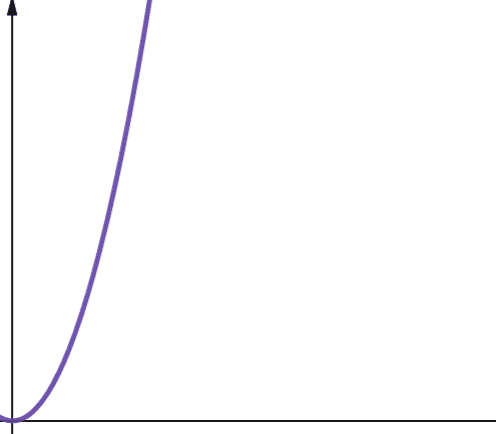
La complexité quadratique est notée O(n²). Si la taille de l’entrée est multipliée par 10, le nombre d’opérations ou l’espace utilisé est multiplié par 10², soit 100. Cette complexité est peu évolutive, car elle croît très rapidement, comme le montre le graphique.

La complexité quadratique apparaît lorsque des boucles imbriquées sont utilisées, par exemple, dans le tri à bulles. Bien que généralement peu souhaitable, il n’est pas toujours possible d’éviter l’utilisation d’algorithmes avec une complexité quadratique.

#6. Polynomiale

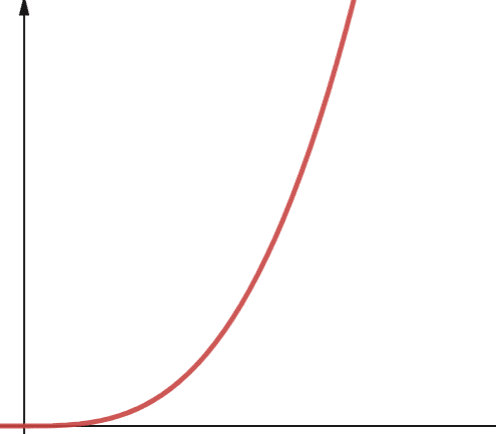
Un algorithme avec une complexité polynomiale est noté O(n^p), où p est un entier constant. p représente l’ordre d’augmentation de n.

Cette complexité apparaît lorsqu’il y a plusieurs boucles imbriquées. La différence entre une complexité polynomiale et quadratique est que la complexité quadratique est de l’ordre de 2, tandis qu’une complexité polynomiale a un ordre supérieur à 2.

#7. Exponentielle

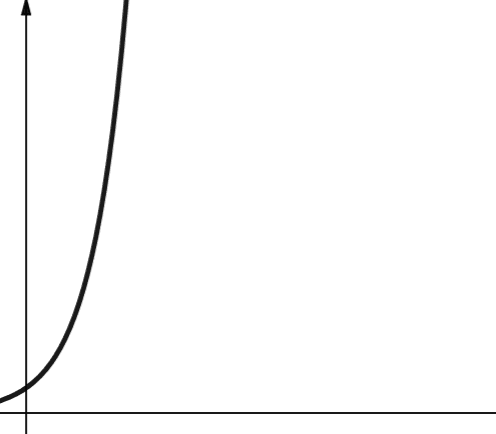
La complexité exponentielle croît plus rapidement que la complexité polynomiale. En mathématiques, la valeur par défaut de la fonction exponentielle est la constante e (nombre d’Euler). En informatique, la valeur par défaut de la fonction exponentielle est 2.

La complexité exponentielle est notée O(2ⁿ). Lorsque n est égal à 0, 2ⁿ est égal à 1. Mais lorsque n augmente jusqu’à 5, 2ⁿ atteint 32. Chaque incrément de n double la valeur précédente. Les fonctions exponentielles sont donc peu évolutives.

#8. Factorielle

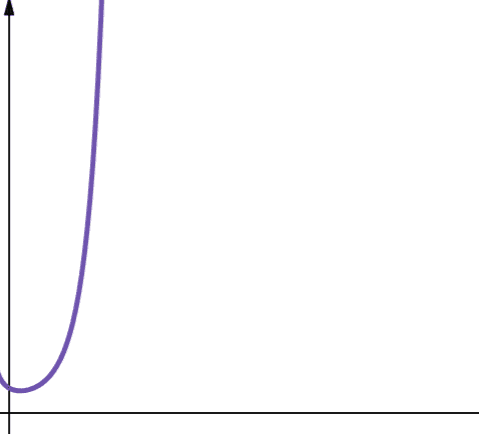
La complexité factorielle est notée O(n!). Cette fonction croît également très rapidement et est donc peu évolutive.

Conclusion

Cet article a présenté l’analyse Big O et expliqué comment la mettre en œuvre. Les différentes complexités ont également été abordées, ainsi que leur évolutivité.

Pour approfondir, vous pouvez vous exercer à effectuer une analyse Big O sur des algorithmes de tri en Python.

0 Partages